TikZ – 06 – Funções

O arroz com feijão das ilustrações de matemática consiste não apenas de geometria, mas também de gráficos de funções. O conceito de função, aliás, encravado no coração de nosso mundo tecnológico, é um dos conceitos centrais de matemática contemporânea. Por isso, oferecemos uma ilustração muito simples, mas bastante rica, para aprendermos como desenhar gráficos de funções em TikZ:

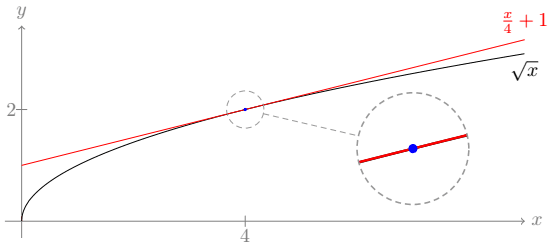
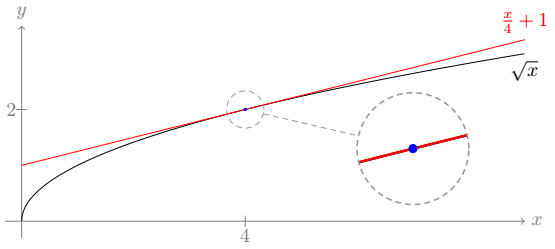
O gráfico mostra as funções f(x)=\sqrt{x} e g(x)=\frac{x}{4}+1 tangenciando-se no ponto P (4,2). Mostra também uma região circular com um zoom no ponto P, indicando que, em um pequeno intervalo ao redor desse ponto, as duas se confundem, e a reta pode ser utilizada como uma ótima aproximação da curva.

Encontrar retas tangentes a curvas contínuas é um dos exercícios mais elementares do cálculo diferencial. Mas como estamos aqui para aprender a desenhar com a TikZ, vamos pular essa parte e ir direto à ilustração.

Desenho

Inicialmente, vamos criar os eixos x e y já com setas, adiantando ligeiramente a parte da decoração:

\begin{tikzpicture}
  \draw [->] (-0.3, 0) -- (9,0);
  \draw [->] (0, -0.3) -- (0,3.5);
\end{tikzpicture}

Você pode escolher outros tamanhos para os eixos, mas aqueles que escolhemos geram a seguinte imagem:

Agora vamos usar o comando plot para traçar os gráficos das funções.

O comando plot

A TikZ provê o comando plot para traçar gráficos de funções elementares, pouco exigentes do ponto de vista computacional. Sua sintaxe exige que você primeiro determine o domínio da função, ou seja, os valor de x que ela toma. Depois, que diga qual é a variável que você usa (em geral, x) e logo depois a fórmula de sua função, que pode ser qualquer uma das muitas que linguagem LaTeX oferece.

Assim, logo depois de um comando \draw, escreva:

\begin{tikzpicture}
  \draw [->] (-0.3, 0) -- (9,0);
  \draw [->] (0, -0.3) -- (0,3.5);
  \draw [domain=0:9] plot (\x,\x^0.5);
\end{tikzpicture}

Essa linha determinou o domínio no intervalo [0, 9] com [domain=0:9], escreveu o comando plot e logo depois determinou que a variável usada seria x (sempre escrita com uma barra invertida antes do x, como \x) e que sua fórmula seria x^{0.5}, a maneira que escrevemos \sqrt{x} usando uma potência fracionária de x . A ilustração fica:

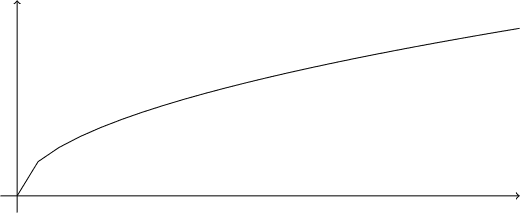
Note que essa curva parece “quebrada” perto da origem. Vamos resolver esse problema depois. Por ora, vamos traçar a reta tangente:

\begin{tikzpicture}
  \draw [->] (-0.3, 0) -- (9,0);
  \draw [->] (0, -0.3) -- (0,3.5);
  \draw [domain=0:9] plot (\x,\x^0.5);
  \draw [domain=0:9] plot (\x,0.25*\x+1);
\end{tikzpicture}

Novamente, o domínio é o intervalo [0, 9] e a fórmula \frac{x}{4}+1 é escrita como 0.25x+1. Em geral, as linguagens de programação usam os símbolos + (mais), – (menos), * (asterisco) e / (barra) para indicar adição, subtração, multiplicação e divisão. E usam o chapéu ^ indicando potência. A figura fica:

Falta uma pequena bolinha nas coordenadas (4, 2). Vamos usar outro comando para desenhá-la.

O comando \filldraw

O ponto de tangência será criado desta vez com um outro comando: \filldraw, que desenha o contorno e preenche a figura ao mesmo tempo. Ele é usado quando queremos combinar \draw com \fill:

\begin{tikzpicture}
  \draw (-0.3, 0) -- (9,0);
  \draw (0, -0.3) -- (0,3.5);
  \draw [domain=0:9] plot (\x,\x^0.5);
  \draw [domain=0:9] plot (\x,0.25*\x+1);
  \filldraw (4,2) circle (0.02);
\end{tikzpicture}

Temos assim:

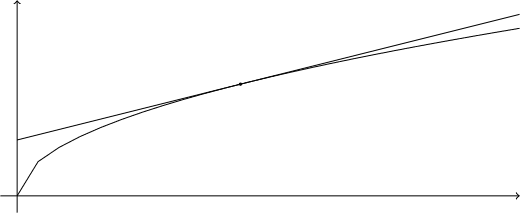
Agora, precisamos desenhar dois pequenos tracinhos nos eixos x e y, indicando as coordenadas (4, 2) do ponto P:

\begin{tikzpicture}
  \draw [->] (-0.3, 0) -- (9,0);
  \draw [->] (0, -0.3) -- (0,3.5);
  \draw [domain=0:9] plot (\x,\x^0.5);
  \draw [domain=0:9] plot (\x,0.25*\x+1);
  \filldraw (4,2) circle (0.02);
  \draw (4, 0.1) -- (4, -0.1);
  \draw (-0.1,2) -- (0.1,2);
\end{tikzpicture}

Preste bem atenção como escrevemos os comandos, pois usaremos essa mesma técnica diversas vezes:

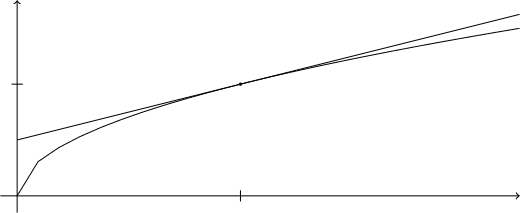
Para finalizar, vamos falar sobre o zoom, criado com a biblioteca spy e os comandos que ela provê.

Dando zoom: a biblioteca spy

Na ilustração, vemos dois círculos: um menor, ao redor do ponto P, e outro maior, mostrando uma ampliação da mesma região. Para fazer isso, devemos primeiro carregar a biblioteca spy no preâmbulo, com \usetikzlibrary{spy}. Ou separando-a com vírgula de outra biblioteca que você já usa, como a calc, fazendo \usetikzlibrary{calc,spy}.

Carregada a biblioteca, você precisará alterar os parâmetros iniciais da figura toda logo após \begin{tikzpicture}:

\begin{tikzpicture}[spy using outlines={magnification=3, size=2cm}] 

Observe que esta linha está entre colchetes. Ela funciona exatamente como fizemos com [scale=5] para ampliar os segmentos no capítulo anterior. Aliás, se você deseja ampliar a figura, você pode usar uma vírgula depois das chaves e acrescentar scale, mas não faremos isso agora.

Os parâmetros que você acrescentou são spy using outlines={magnification=3, size=2cm}. Isso significa que você vai acessar a biblioteca spy usando (using) contornos (outlines) que ampliarão 3 vezes (magnification=3) a região focada e a apresentarão em uma outra região de tamanho igual a 2cm (size=2cm).

Mas qual é a região focada (o círculo menor) e onde você colocará o zoom (o círculo maior)? Isso é feito com a linha seguinte acrescentada normalmente no programa:

\spy on (4,2) in node at (7,1.3); 

Ela significa: “faça foco no (spy on) ponto (4,2) e coloque a ampliação nas coordenadas (in node at) (7, 1.3)”. Com isso, o seu programa fica:

\begin{tikzpicture}[spy using outlines={magnification=3, size=2cm}]
  \draw [->] (-0.3, 0) -- (9,0);
  \draw [->] (0, -0.3) -- (0,3.5);
  \draw [domain=0:9] plot (\x,\x^0.5);
  \draw [domain=0:9] plot (\x,0.25*\x+1);
  \filldraw (4,2) circle (0.02);
  \draw (4, 0.1) -- (4, -0.1);
  \draw (-0.1,2) -- (0.1,2);
  \spy on (4,2) in node at (7,1.3);
\end{tikzpicture}

E sua ilustração é:

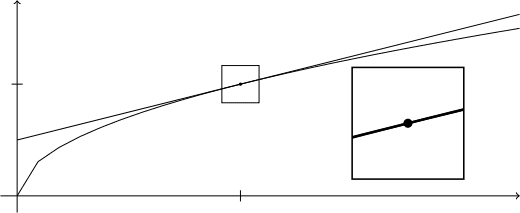
Ainda não é um círculo tracejado, mas vamos chegar lá. Já é possível ver a ampliação da região ao redor do ponto (4, 2), e perceber como as curvas são praticamente indistintas. Isso que nos possibilita usar uma no lugar da outra para cálculos com valores próximos de 4. Por exemplo, você pode até tirar a raiz de 4.1 de cabeça, com boa precisão, usando a fórmula da reta g(x) = \frac{x}{4}+1. Basta dividir 4.1 por 4, o que dá 1.025, e somar 1, obtendo 2.025. Na calculadora, a raiz de 4.1 é 2.0248, apenas dois décimos de milésimo menor que nossa aproximação. Nada mal, não é?

Texto

Vamos desenhar os textos com o comando node {$ ... $}, acrescentando dentro dos dois cifrões as fórmulas em LaTeX de que precisamos. Até as letras e os números serão acrescentados assim para uniformização visual:

\begin{tikzpicture}
  [spy using outlines={magnification=3, size=2cm}]
  \draw [->] (-0.3, 0) -- (9,0) node {$x$};
  \draw [->] (0, -0.3) -- (0,3.5) node {$y$};
  \draw [domain=0:9] plot (\x,\x^0.5) node {$\sqrt{x}$};
  \draw [domain=0:9] plot (\x,0.25*\x+1) node {$\frac{x}{4}+1$};
  \filldraw (4,2) circle (0.02);
  \draw (4, 0.1) -- (4, -0.1) node {$4$};
  \draw (-0.1,2) -- (0.1,2) node {$2$};
  \spy on (4,2) in node at (7,1.3);
\end{tikzpicture}

Temos, como sempre, os textos “embolados” com os outros elementos:

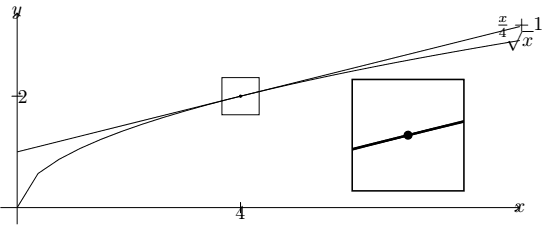
A fase de decoração resolverá isso rapidamente. Por ora, perceba apenas que escrevemos \sqrt{x} para \sqrt{x} e \frac{x}{4} para escrever \frac{x}{4} (sim, você precisa saber um pouquinho de LaTeX para decifrar essas fórmulas, como dissemos na introdução…).

Decoração

Primeiro, os textos. Como sempre, os parâmetros que escolhemos são apenas uma sugestão, e você deve testar outras opções:

\begin{tikzpicture}
  [spy using outlines={magnification=3, size=2cm}]
  \draw [->] (-0.3, 0) -- (9,0) node [right] {$x$};
  \draw [->] (0, -0.3) -- (0,3.5) node [above] {$y$};
  \draw [domain=0:9] plot (\x,\x^0.5) node [below] {$\sqrt{x}$};
  \draw [domain=0:9] plot (\x,0.25*\x+1) node [above] {$\frac{x}{4}+1$};
  \filldraw (4,2) circle (0.02);
  \draw (4, 0.1) -- (4, -0.1) node [below] {$4$};
  \draw (-0.1,2) -- (0.1,2) node [left] {$2$};
  \spy on (4,2) in node at (7,1.3);
\end{tikzpicture}

Temos:

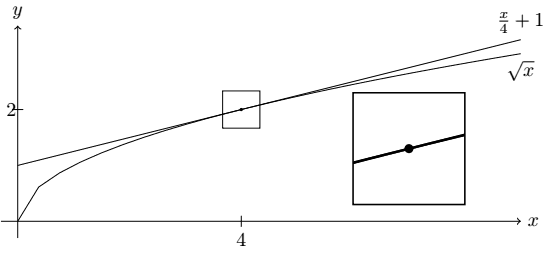
Observe que o número 2 no eixo y está “colado” no tracinho. Vamos ajustar isso depois. Agora é hora de colorir!

Os eixos, a reta tangente, a bolinha do ponto P e os tracinhos sobre os eixos ganharam as seguintes cores, que você pode (e deve) alterar para criar algo mais bonito:

\begin{tikzpicture}
  [spy using outlines={magnification=3, size=2cm}]
  \draw [->, gray] (-0.3, 0) -- (9,0) node [right] {$x$};
  \draw [->, gray] (0, -0.3) -- (0,3.5) node [above] {$y$};
  \draw [domain=0:9] plot (\x,\x^0.5) node [below] {$\sqrt{x}$};
  \draw [domain=0:9, red] plot (\x,0.25*\x+1) node [above] {$\frac{x}{4}+1$};
  \filldraw [blue] (4,2) circle (0.02);
  \draw [gray] (4, 0.1) -- (4, -0.1) node [below] {$4$};
  \draw [gray] (-0.1,2) -- (0.1,2) node [left] {$2$};
  \spy on (4,2) in node at (7,1.3);
\end{tikzpicture}

E temos uma figura próxima à que queremos:

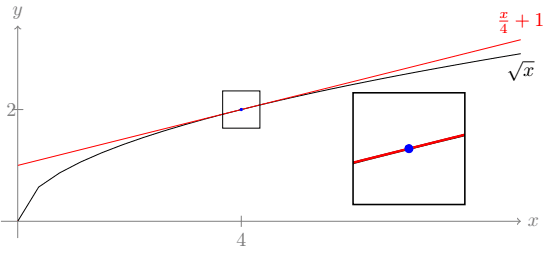
Muita coisa pode ser melhorada. Vamos a um ajuste fino desses elementos gráficos.

Ajuste fino para texto

As posições dos textos não precisam estar restritas a above, below, left e right. Usar apenas esses parâmetros deixa os números 4 e 2 afastados ou próximos demais de suas marcas nos eixos. Mas podemos acrescentar ou retirar espaço em relação a um determinado ponto da seguinte maneira:

 \draw [gray] (4, 0.1) -- (4, -0.1) node [below=-2pt] {$4$};
 \draw [gray] (-0.1,2) -- (0.1,2) node [left=2pt] {$2$}; 

Isso nos dá a figura a seguir, com uma localização muito mais fina dessas coordenadas:

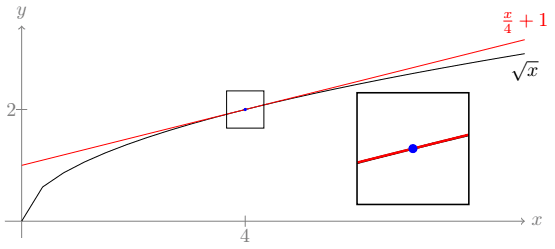
Ficou sutilmente melhor com o acréscimo ou a retirada de 2 pontos nas distâncias padrão.

Agora, vamos estilizar o zoom, fazendo com que o quadrado se torne um círculo (circle) com 80% da cor cinza (gray!80) e densamente tracejado (densely dashed). Vamos também unir as regiões com connect spies:

  [spy using outlines={circle, gray!80, densely dashed, magnification=3, size=2cm, connect spies}]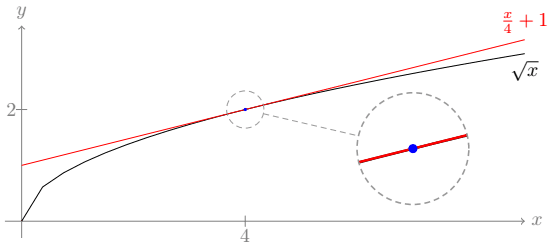

Quase acabando. Precisamos agora resolver o problema da suavização da curva, retirando o “quebrado” que vemos perto da origem. Vamos fazer isso alterando o parâmetro samples e usando inteligentemente o próprio zoom para ampliar regiões problemáticas.

Suavizando com samples

A TikZ constrói uma curva dividindo o domínio em 25 partes, calculando a “altura” da curva em um ponto de cada uma dessas partes e depois unindo tudo com segmentos de reta. Toda curva é, portanto, uma coleção de segmentos de retas unidos consecutivamente. Por isso é que você vê “quebras” nas curvas.

Vamos aumentar de 25 para 250, dez vezes mais, o número de partes em que o domínio é dividido. Isso é feito com o acréscimo do parâmetro samples=250 logo depois do domínio da curva problemática:

\draw [domain=0:9, samples=250] plot (\x,\x^0.5) node [below] {$\sqrt{x}$}; 

A palavra samples significa amostras, que é o nome técnico dado aos pontos que escolhemos para construir a curva.

Mas dividir o domínio em 250 partes pode não ser suficiente. Por isso, vamos ser espertos e usar o próprio zoom par anos auxiliar com visualização de partes problemáticas. No caso da curva da raiz quadrada, vamos alterar o foco para a origem (0, 0) e ver o que acontece por lá:

\spy on (0,0) in node at (7,1.3); 

Isso nos dá a imagem a seguir:

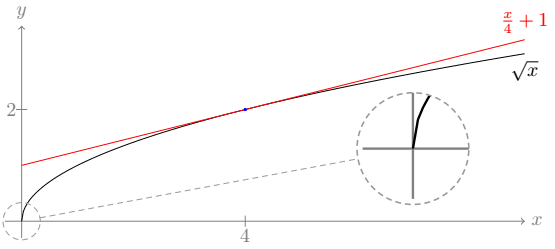
Observe que a curva está muito mais suave. Os “quebrados” não são perceptíveis sem zoom. Mesmo assim, o zoom mostra uma pequena “quebra” perto da origem. Você pode querer eliminá-lo, testando com 500, 750 ou mesmo 1000 amostras. Vamos ver se 1500 amostras são suficientes, ou seja, vamos fazer samples=1500:

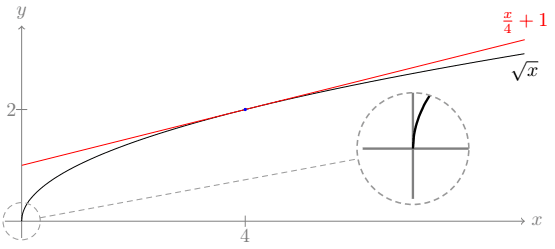
Parece ótimo. Vamos deixar assim e voltar nosso foco para o ponto (4,2), o que nos dará a imagem final:

Eis aqui o código todo:

\begin{tikzpicture}
  [spy using outlines={circle, gray!80, densely dashed, magnification=3, size=2cm, connect spies}]
  \draw [->, gray] (-0.3, 0) -- (9,0) node [right] {$x$};
  \draw [->, gray] (0, -0.3) -- (0,3.5) node [above] {$y$};
  \draw [domain=0:9, samples=1500] plot (\x,\x^0.5) node [below] {$\sqrt{x}$};
  \draw [domain=0:9, red] plot (\x,0.25*\x+1) node [above] {$\frac{x}{4}+1$};
  \filldraw [blue] (4,2) circle (0.02);
  \draw [gray] (4, 0.1) -- (4, -0.1) node [below=-2pt] {$4$};
  \draw [gray] (-0.1,2) -- (0.1,2) node [left=2pt] {$2$};
  \spy on (4,2) in node at (7,1.3);
\end{tikzpicture}

Vale observar que não é aconselhável usar número muito grandes com samples, pois isso exigirá da TikZ muitos cálculos, ocasionando diversos erros. Por isso, teste números menores como 250 e 500 para ver se são suficientes. Note também que a reta não precisou disso. Em verdade, ela nem precisaria das 25 amostrar que a TikZ usa por padrão, mas apenas de duas: os pontos inicial e final.

Resumo

Desenho

• \draw [domain=a:b] plot (\x, fórmula com \x) – desenha (draw) um gráfico (plot) com domínio (domain) entre a e b, usando \x como variável dentro de uma fórmula escrita em LaTeX.

Texto

• + - * ^ – em LaTeX, representam as operações de adição, subtração, multiplicação e exponenciação
• \frac{n}{d} – em LaTeX, escreve a fração \frac{n}{d}
• \sqrt{x} – em LaTeX, escreve a raiz de x

Decoração

• \usetikzlibrary{spy} – carrega a biblioteca spy
• spy using outlines – essas palavras indicam que você vai dar um zoom usando os parâmetros seguintes.
• dashed, densely dashed e loosely dashed – tracejado, com opções de ser densamente tracejado e fracamente tracejado.
• magnification=n – ampliação em n vezes
• size=n – tamanho da região de zoom, em geral em n centímetros.
• connect spies – conecta a região de foco com a região de ampliação.
• samples=n – divide um domínio em n partes para criar pontos que serão conectados com segmentos de reta. Se o número de pontos for grande, o traçado parecerá uma curva suave.
• above=2pt – ajuste fino de localização com nodes. Neste caso, acrescenta mais 2 pontos (2pt) entre o node e o texto. Obviamente, pode ser usado com below, left e right e pode conter distâncias negativas.
• \spy on (a, b) in node at (c,d) – faz zoom ao redor de (a, b) e o projeta no ponto (c, d).

Exercícios

Que tal brincar um pouco com os parâmetros da ilustração?

• Nos parâmetro iniciais, mude magnification para 5 e size para 3 cm. Coloque o círculo maior em cima do ponto, e não do lado.
• Retire connect spies e troque densely dashed por dotted. Você prefere assim?
• Mude samples para 10, depois para 5, depois para 3 e depois para 2. Você conseguiu entender que a curva é feita de segmentos de reta?
• Mude os domínios de cada curva. Tente domain=0:5 e depois tente domain=-1:10. Observe que, neste último caso, a TikZ traça uma curva invertida para a raiz, mesmo sabendo que não existe raiz quadrada de número negativo (no conjunto dos números reais). Como você acha que ela faz?
• No parâmetros iniciais, dê uma vírgula no final e acrescente scale=2. O que aconteceu? Será que tudo aumentou duas vezes?

DESAFIO!

Seu desafio é repetir a ilustração a seguir, bem mais simples do que a que acabamos de realizar:

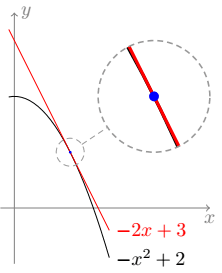
Você conseguiria calcular o ponto de tangência? Se não, não se preocupe: tente “no olho”, por tentativa e erro. Depois confira nas equações se você acertou.

Observe que as cores preta e vermelha das curvas ressaltam bem a aproximação que uma faz da outra. Há uma ligeira discrepância, um pouquinho de preto embaixo do vermelho, indicando que elas obviamente não são idênticas, mas que que quase chegam lá quando verificamos ali pertinho do ponto…