TikZ – 07 – Repetição

Muitas vezes, ilustrações apresentam elementos repetidos. Lidar com eles sem que nossa tarefa se torne cansativa e desanimadora é o objetivo deste capítulo, para o qual preparamos a seguinte ilustração:

Essa ilustração tenta, com muito boa vontade, mostrar o conjunto (infinito) dos números inteiros que distam uns dos outros por múltiplos de 3, a partir do número 1. Em termos puramente matemáticos, temos uma representação da classe de números inteiros congruentes a 1 com módulo 3 ou, falando ainda mais claramente, a classe de inteiros que deixam resto 1 quando divididos por 3.

Por mais interessante que seja a matemática representada na ilustração, o que propriamente nos interessa aqui são suas características repetitivas. Observe como se repetem os pequenos tracinhos, os círculos vermelhos e os números acima e abaixo. Todos esses elementos serão traçados não um a um, mas através de um subterfúgio comum a todas as linguagens de programação: os laços de repetição.

Desenho

Vamos começar desenhando o eixo. Como antes, vamos já traçar a setinha do lado direito:

\begin{tikzpicture}
  \draw [->] (-5.5, 0) -- (7.5, 0);
\end{tikzpicture}

Esse código gera a imagem:

Os elementos que mais se repetem nessa imagem são os tracinhos que marcam a posição dos números no eixo:

Como fazer isso sem ter que escrever dezenas de linhas com códigos, uma para cada tracinho? Vamos usar o laço de repetição foreach.

O laço \foreach

Laços de repetição são elementos comuns em linguagens de programação. A TikZ tem seu laço particular – chamado de foreach – que significa “para cada”.

Antes de explicar como ele funciona, vamos apresentar o código que gerou as marquinhas no eixo:

\begin{tikzpicture}
  \draw [->] (-5.5, 0) -- (7.5, 0);
  \foreach \x in {-5,...,7}
    \draw (\x, -0.05) -- (\x, 0.05);
\end{tikzpicture}

Com essas duas novas linhas, temos a ilustração já apresentada acima:

Como funciona esse laço de repetição? em primeiro lugar, vamos desvendar a primeira linha:

\foreach \x in {-5,...,7}

O comando foreach significa, literalmente, “para cada”. A expressão {-5, ..., 7} é uma abreviação do conjunto {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7}, ou seja, os treze números inteiros que vão de -5 a 7. Assim, a expressão pode ser traduzida como “para cada x no conjunto {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7}“. Mas o que isso quer dizer?

Isso nos diz que temos uma variável x que vai tomar sucessivamente os valores do conjunto dado e vai fazer alguma coisa com esse valor. Em nosso caso, essa variável vai levar os valores do conjunto, um de cada vez, para dentro da expressão

\draw (\x, -0.05) -- (\x, 0.05);

que, por sua vez, vai traçar as marquinhas no eixo. Como?

Em primeiro lugar, x vai valer -5, que é o primeiro elemento do conjunto. Esse valor será substituído em todos os lugares onde x aparece no comando \draw. Ou seja, com x igual a -5, esse comando será:

\draw (-5, -0.05) -- (-5, 0.05);

Com isso, teremos desenhado o primeiro tracinho sobre o eixo, aquele mais à esquerda, na posição x = -5. Logo depois, o laço foreach vai trocar o valor de x pelo próximo do conjunto, ou seja, x vai valer -4. E, novamente, vai substituir no comando \draw esse valor:

\draw (-4, -0.05) -- (-4, 0.05);

Agora, é o segundo tracinho que será marcado sobre o eixo, na posição x = -4. E assim será, sucessivamente, até que todos os elementos do conjunto sejam esgotados. Quando o último elemento do conjunto for usado, o laço acaba, e teremos a imagem do eixo com as marcações.

Não entendeu? Vamos para o segundo laço, que vai desenhar as bolinhas referentes aos números -5, -2, 1, 4 e 7, uma sequência em que o próximo número está separado do anterior por 3 unidades, ou seja, “pula” 3 de cada vez. O código é o seguinte:

\begin{tikzpicture}
  \draw [->] (-5.5, 0) -- (7.5, 0);
  \foreach \x in {-5,...,7}
    \draw (\x, -0.05) -- (\x, 0.05);
  \foreach \x in {-5,-2,...,7}
    \filldraw (\x, 0) circle (0.07);
\end{tikzpicture}

Agora o conjunto do qual x vai tomar seus valores será {-5, -2, 1, 4, 7}. Por quê? O que mudou? Observe que escrevemos {-5, -2, … 7}:

\foreach \x in {-5,-2,...,7}

Isso indica à TikZ que depois do -5 deve vir o -2, estabelecendo um “pulo” de 3 unidades. E isso será estendido para todos os números do conjunto, começando em -5 e “pulando” de 3 em 3.

Os círculos em si serão desenhados com a linha:

\filldraw (\x, 0) circle (0.07);

Ou seja, círculos de raio 0.07 nas posições (-5, 0), (-2, 0), (1, 0), (4, 0) e (7, 0). Isso vai gerar a seguinte figura:

Mais um laço de repetição será usado para traçar as setas que apontam dos círculos até o conjunto {…, -5, 2, 1, 4, 7, …}. Vamos usar o laço seguinte:

\begin{tikzpicture}
  \draw [->] (-5.5, 0) -- (7.5, 0);
  \foreach \x in {-5,...,7}
    \draw (\x, -0.05) -- (\x, 0.05);
  \foreach \x in {-5,-2,...,7}
    \filldraw (\x, 0) circle (0.07);
  \foreach \x in {-5,-2,...,7}
    \draw (\x, -0.5) -- (0.9+0.1*\x,-2);
\end{tikzpicture}

Novamente, o conjunto de partida é o {-5, -2, -1, 4, 7}. E as setas serão traçadas por:

\draw (\x, -0.5) -- (0.9+0.1*\x,-2);

Mas o que significa aquela expressão 0.9+0.1*\x dentro dos parênteses? Acredite: é melhor que você, agora, altere cada um de seus valores e reexecute o programa para entender exatamente o que ela faz. Por exemplo, troque 0.9 por 1.3, execute o programa e veja o que aconteceu. Agora, altere 0.1 por 0.5, execute e veja novamente o que aconteceu. Assim você vai entendendo o que cada número desses faz.

Como em toda ilustração, às vezes a gente precisa testar muitas coisas, ver os erros que comentemos e ir ajustando até encontrar uma solução ideal. Essa fórmula foi encontrada assim, com alguma matemática no meio do caminho.

Com esse novo código, temos:

As linhas do desenho estão traçadas. Vamos passar para o texto.

Texto

Vamos aproveitar o primeiro laço foreach e usar node para escrever o texto logo após as primeiras coordenadas do draw:

\begin{tikzpicture}
  \draw [->] (-5.5, 0) -- (7.5, 0);
  \foreach \x in {-5,...,7}
    \draw (\x, -0.05) node [above=2pt] {\x} -- (\x, 0.05);
  \foreach \x in {-5,-2,...,7}
    \filldraw (\x, 0) circle (0.07);
  \foreach \x in {-5,-2,...,7}
    \draw (\x, -0.5) -- (0.9+0.1*\x,-2);
\end{tikzpicture}

A expressão node [above=2pt] {\x} significa que vamos escrever um texto 2 pontos acima das coordenadas, e o texto será o valor de x do laço. Essa decoração deveria ficar para o fim, segundo nossa metodologia, mas isso não é uma lei do universo: às vezes, se já sabemos como a figura deve aparentar, já colocamos as decorações junto com tudo o mais.

Esse pequeno acréscimo no código gera:

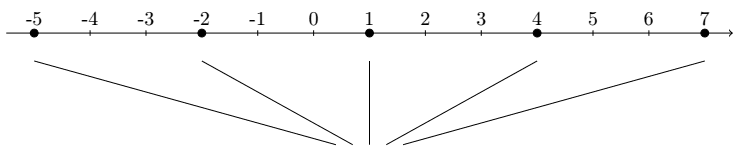
Vamos criar um quarto laço para escrever a segunda série de números, aqueles que vão ficar abaixo do eixo, destacando os pontos marcados com uma bolinha:

\begin{tikzpicture}
  \draw [->] (-5.5, 0) -- (7.5, 0);
  \foreach \x in {-5,...,7}
    \draw (\x, -0.05) node [above=2pt] {\x} -- (\x, 0.05);
  \foreach \x in {-5,-2,...,7}
    \filldraw (\x, 0) circle (0.07);
  \foreach \x in {-5,-2,...,7}
    \draw (\x, -0.5) -- (0.9+0.1*\x,-2);
  \foreach \x in {-5,-2,...,7}
    \draw (\x, 0) node {\x};
\end{tikzpicture}

O código acrescentado é um laço que simplesmente escreve o valor de x nas coordenadas indicadas. Poderíamos ter aproveitado um laço anterior, mas resolvemos escrever outro apenas por questões de clareza. E temos a figura:

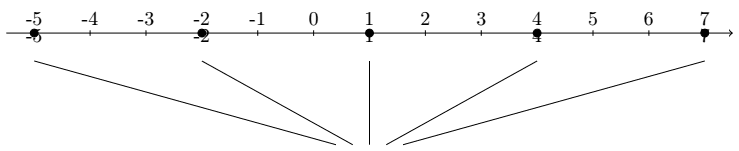
Mais adiante vamos ajustar a posição dos números. Por ora, acrescente no fim do código a seguinte linha, que desenha o conjunto abaixo das setas:

\draw (1, -2.3) node {\{\ldots, -5, -2, 1, 4, 7, \ldots\}}; 

Com essa linha (que tem um pouco de LaTeX), criamos a figura:

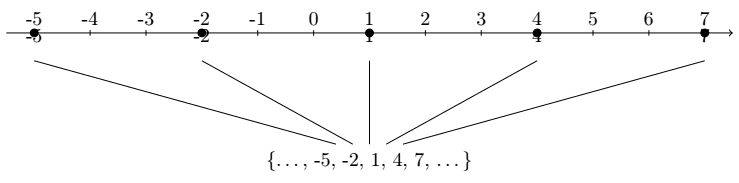
Bastam alguns ajustes e tudo ficará como queremos.

Decoração

Primeiro, vamos ajustar aposição e a cor dos números de baixo acrescentando [below,red] no último laço:

\foreach \x in {-5,-2,...,7}
  \draw [below, red] (\x, 0) node {\x};

Isso gera:

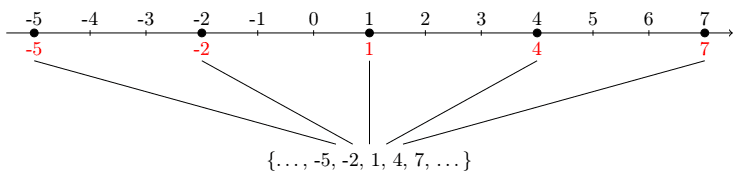
Agora, vamos colorir as bolinhas acrescentando [red] no segundo laço:

\foreach \x in {-5,-2,...,7}
  \filldraw [red] (\x, 0) circle (0.07);

E temos a imagem:

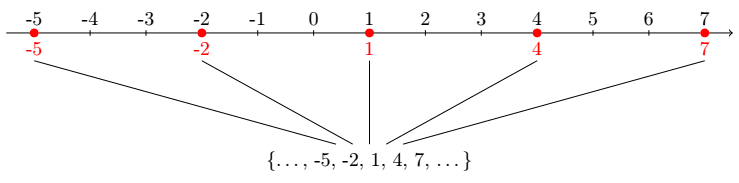
Para finalizar, vamos acrescentar [->, dotted] na setas, que são produzidas pelo terceiro laço foreach:

\foreach \x in {-5,-2,...,7}
  \draw [->, dotted](\x, -0.5) -- (0.9+0.1*\x,-2);

E, assim, temos a figura final:

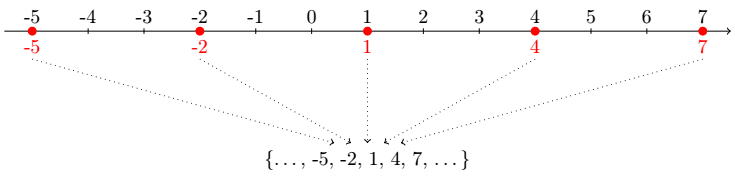
O código todo:

\begin{tikzpicture}
  \draw [->] (-5.5, 0) -- (7.5, 0);
  \foreach \x in {-5,...,7}
    \draw (\x, -0.05) node [above=2pt] {\x} -- (\x, 0.05);
  \foreach \x in {-5,-2,...,7}
    \filldraw [red] (\x, 0) circle (0.07);
  \foreach \x in {-5,-2,...,7}
    \draw [->, dotted](\x, -0.5) -- (0.9+0.1*\x,-2);
  \foreach \x in {-5,-2,...,7}
    \draw [below,red] (\x, -0.05) node {\x};
  \draw (1, -2.3) node {\{\ldots, -5, -2, 1, 4, 7, \ldots\}};
\end{tikzpicture}

Resumo

Desenho

• \foreach \x in {-5,...,7} – para cada x no conjunto {-5, …, 7}, a TikZ realiza a ação da linha seguinte. Observe que não há ponto-e-vírgula nessa linha, mas apenas no fim da linha seguinte.
• \foreach \x in {-5,-2,...,7} – para cada x no conjunto {-5, -2, …, 7}, em que os dois primeiros números indicam o “salto” a ser dado no conjunto, a TikZ realiza a ação da linha seguinte. No caso, o salto tem o valor 3.

Texto

• \{ \ldots, -5, -2, 1, 4, 7, \ldots \} – código LaTeX que gera o conjunto indicado. A expressão \ldots cria os três pontos.

Decoração

• [above=2pt] – ajuste fino: coloca o texto de 2 pontos acima das coordenadas.

Exercícios

• Mude os números vermelhos para cima e os pretos para baixo, e “inverta” o desenho, colocando as setas apontando para cima, onde você vai colocar o conjunto {…, -5, -2, 1, 4, 7, …}
• Tente alterar o desenho para que o conjunto representado seja não {…, -5, -2, 1, 4, 7, …}, mas {…, -4, -1, 2, 5, 8, …}, ou seja, o conjuntos dos números que deixam 2 quando divididos por 3.
• Coloque o desenho na vertical, com a reta numérica à esquerda e as setas que selecionam os números apontando da esquerda para a direita, onde estará escrito o conjunto.

DESAFIO!

O desafio é fazer um desenho que represente os 3 conjuntos {…, -5, -2, 1, 4, 7, …}, {…, -4, -1, 2, 5, 8} e {…,-6, -3, 0, 3, 6, …} em que o primeiro é o dos números que deixam resto 1 quando divididos por 3; o segundo, o dos números que deixam resto 2 quando divididos por 3; e o terceiro, o dos múltiplos de 3, ou seja, que deixam resto 0 quando divididos por 3.

Mantenha o vermelho para o primeiro conjunto, use azul para o segundo e o verde para o terceiro. Faça três conjuntos de setas, da melhor maneira que você conseguir, ou tente representar os conjuntos de outra maneira.